Fractions
Remember the basics about fractions that you have learnt through Key Stage 3:
Simplifying / equivalent fractions means that BOTH the numerator and the denominator have to be dealt with in the same way – i.e. if you double one then you must double the other; if you divide one by 8, then the other must be divided by the same amount.
The numerator must always be smaller than the denominator, unless you have been told that the answer needs to be given as a top heavy/improper fraction.
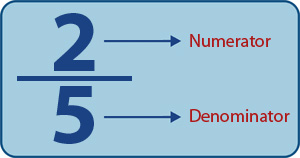
Fractions are a portion or part of a something.
Example:
A selection box contains four types of sweets: 6 chocolates, 7 caramels, 3 bonbons, and 4 nougats.
- What fraction are chocolate?
- What fraction are not chocolate?
Answer:
First calculate the total number of sweets is the selection box.
Total number of sweets = 6+7+3+4 = 20
-
Number of chocolates = 6
620 , 6 out of 20 sweets are chocolate.
This can be cancelled down to 310 by dividing the top and bottom by 2.
These are equivalent fractions.
-
Number of sweets that are not chocolates = 20−6=14
1420 , 14 out of 20 sweets are not chocolate.
This can be cancelled down to 710 by dividing the top and bottom by 2.
Equivalent fractions
Equivalent fractions are fractions that look different but show exactly the same amount.
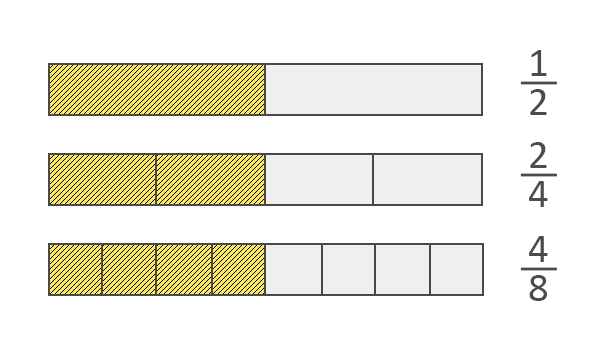
Equivalent fractions can be made by multiplying or dividing the numerator AND denominator by the SAME number.
12
24
12
48
Fractions can be simplified by dividing the numerator and denominator by the same number. This is called cancelling.
860
215
Improper fractions
Improper fractions or ‘top heavy’ fractions are fractions in which the numerator is larger than the denominator, e.g. 73, 52, 139.
Converting Improper Fractions to Mixed Fractions
To convert an improper fraction to a mixed fraction, follow these steps:
Step 1: Divide the numerator by the denominator.
Step 2: Write down the whole number answer.
Step 3: Then write down any remainder above the original denominator.
Example:
Convert 73 to a mixed fraction.
This can be written as a mixed fraction in the following way.
Divide:
7 ÷ 3 = 2 with a remainder of 1.
We then write down the 2 and then the remainder 1 is written as a fraction with the original denominator (which was 3).
So, 73 = 2 13
Converting Mixed Fractions to Improper Fractions
To convert a mixed fraction to an improper fraction, follow these steps:
Step 1: Multiply the whole number part by the fraction's denominator.
Step 2: Add that to the numerator.
Step 3: Then write the result on top of the denominator.
Example:
Convert 4 25 to an improper fraction.
Multiply the whole number by the denominator: 4 x 5 = 20
Add this to the numerator: 20 + 2 = 22
Then write this above the denominator: 225
